Francis Perrin’s early-1939 analysis of uranium criticality: a look back
Introduction

Figure 1. Francis Perrin (1902-1992) in 1951, Source: AIP Emilio Segrè Visual Archives, Physics Today Collection
In the May 1, 1939, edition of Comptes Rendus, the weekly journal of the French Academy of Sciences, physicist Francis Perrin (1901-1992; Fig. 1) of the Collège de France published a 3-page paper containing the first numerical estimate of the critical mass necessary to achieve a fast-neutron chain reaction in a natural-abundance uranium compound [1]. His result was about 40 metric tonnes (40,000 kg), which he estimated could be reduced to about 12 tonnes with a suitable tamper. He did not seem particularly concerned with the enormous scale of this result – which would later prove to be about three orders of magnitude too large – but he did remark that since a fast-neutron reaction would not be easy to control, a better hope might be to use hydrogenic compounds to slow neutrons and so achieve a controllable reaction.
Perrin’s calculation was soon eclipsed by deeper understanding of the mechanism of fission; it had no real relevance for a Hiroshima-type nuclear weapon, which requires essentially pure U-235. He was, however, apparently the first to publish a diffusion-theory-based quantitative estimate of the critical mass (“masse critique”), so it is interesting to take a retrospective look at his work to see both how his numbers arose and to explore the impact of his paper. As I will show, Perrin’s physics was largely correct: Had he considered using pure U-235 and been armed with even rough numbers for the relevant cross-sections, he could have made a quite respectable estimate of the critical mass for a nuclear weapon nearly a year before Otto Frisch and Rudolf Peierls alerted British authorities to the possibility of “super-bombs” in their famous memorandum of March, 1940 [2]. In this article I examine Perrin’s model, make some speculations as to the provenance of his parameter values, and consider how his work compared to later efforts.
Perrin’s criticality model
To set the context of Perrin’s work, it is helpful to briefly summarize what was known of fission in the spring of 1939. Otto Hahn and Fritz Strassmann had discovered fission via slow (moderated) neutron bombardment of uranium, but Perrin considered fast neutrons, a choice which may have been conditioned by the fact that he would not have to deal with the complicating effects of a moderator; also, it is clear from the outset of his paper that he was interested in the possibility of explosively liberating large amounts of energy (“libérant une énergie énorme”). In February, 1939, Niels Bohr posited that it was the rare 235 isotope of uranium that was responsible for slow-neutron fission; perhaps Perrin was thinking that the much more abundant 238 isotope might suffer fast-neutron fission if there was some energy threshold involved. Bohr’s hypothesis had been made in response to the differing fission properties of thorium and uranium uncovered by Otto Frisch and others [3, 4]; Perrin referenced neither Frisch nor Bohr, but it is hard to imagine that he would have been unaware of their work. Further research over the following year by Bohr and John Wheeler (among others) would reveal the poisoning role of inelastic scattering and capture of neutrons by U-238.
Perrin considered uranium oxide (U3O8) of natural isotopic abundance, and treated a chain reaction as an application of diffusion theory, exactly the appropriate physics. He would have come to diffusion physics from years of expertise: his father, Jean Perrin, was awarded the 1926 Nobel Prize for Physics for his experimental determination of Avogadro’s number, and Perrin fils’ 1928 doctoral thesis was on the topic of Brownian motion [5].
Perrin considered the simplifying case where the mean free path of the neutrons is small in comparison to the characteristic size of the sample. While not strictly true for nuclear weapons materials, this is a commonly-made and reasonably accurate assumption. This allowed him to write a simple expression for the mean free path in terms of the number densities of uranium and oxygen atoms and their cross-sections for neutron transport and fission; this is equation (2) below. His terminology is somewhat confusing in that he uses the term “absorption” to refer to both the fission cross-section of uranium and the capture cross-section of a tamper material or the oxygen in U3O8, and defines what we now call the transport cross-section, the sum of the cross-sections for fission (if possible) and elastic scattering, as the “diffusion” cross-section. Details of solving the diffusion equation can be found in [6]. Doing so for a spherical system along with the boundary condition that criticality occurs when the neutron density at the edge of the sphere falls to zero, he arrived at an explicit expression for the critical radius:
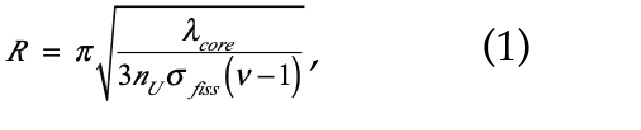
where nU is the number density of uranium atoms, v is the number of neutrons emitted per fission, and 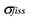
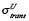
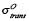
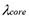
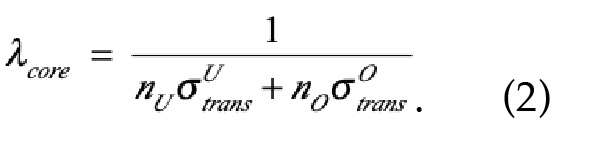
nU and nO are computed by first computing the number density of U3O8 molecules from its known bulk density and atomic weight, and multiplying by factors of three and eight. The true density of U3O8 is about 8.4 gr cm-3; Perrin assumed 4.2 gr cm-3.
Equation (1) appeared in Robert Serber’s Los Alamos Primer four years later, in April, 1943 [7]. As Serber explained, demanding that the neutron density goes to zero at the edge of the bomb core is too restrictive a condition, and ends up leading to overestimating the critical mass. However, it does have the advantage that it leads to equation (1) for the critical radius; otherwise, one has to deal with a transcendental equation.
Perrin adopted 
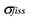
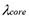
But for his density and fission cross-section, Perrin’s numbers are respectably close to what we would use today for U-235. The source of his fission cross-section may have been a paper by Herbert Anderson and his collaborators at Columbia University which appeared in the March 1, 1939, edition of the Physical Review, where they report precisely the figure of 0.1 barns for natural-abundance uranium [8]. Perrin does not reference Anderson et al., nor does he give any source for his transport cross-sections. A paper published in the April 15, 1939 Physical Review by Anderson, Fermi, and Hanstein did report a total capture cross-section for uranium of about 5 barns, but this was for slow neutrons [9]. Perrin does refer to a paper published by Hans von Halban and collaborators in the April 22, 1939, edition of Nature wherein they reported v ~ 3.5 + 0.7 neutrons per fission [10]. In view of the still-unfolding understanding the roles of U-235 and U-238 in the fission process, we cannot be critical of Perrin’s small fission cross-section. Curiously, Frisch and Peierls would err in the opposite direction by assuming too large a fission cross-section for U-235, 10 barns, and significantly underestimating the critical mass. Since the critical radius behaves as 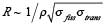
Effect of tamper
Perrin then turns to the idea of surrounding the fissile core with a spherical metallic neutron-reflective tamper of thickness L. This has the effect of lowering the critical mass by returning neutrons that would otherwise escape back into the core and giving them fresh opportunities to induce fissions. He then presented the following transcendental equation for the critical radius R:
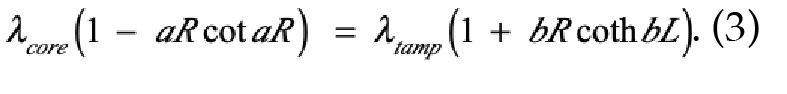
Here, 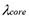
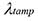
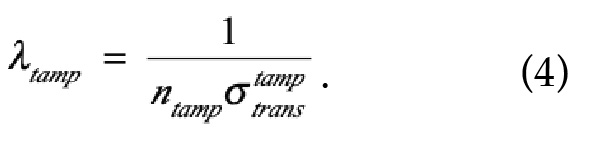
a and b both have units of inverse length, and depend on the properties of the core and tamper materials. But for a factor of 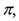
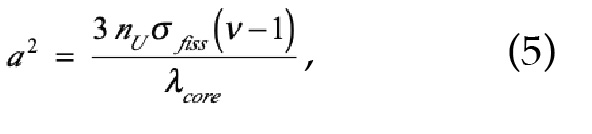
and
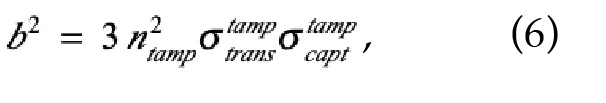
where 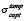
By considering the analysis of tamped cores presented in ref. [6], I have determined that equation (3) results from a standard solution to the neutron-diffusion equation in conjunction with assuming the continuity of the neutron density and flux at the core/tamper interface and that the neutron density goes to zero at the outer edge of the tamper, again a more restrictive but simpler condition than what applies in actuality. Perrin chose iron as the tamper, taking a thickness of 35 centimeters, and adopting 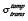
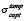
Subsequent developments
Two other papers on critical conditions soon followed Perrin’s. In the June 6, 1939, edition of Naturwissenschaften, Seigfried Flügge presented a much lengthier analysis of the prospects for realizing nuclear energy [11]. He was much more concerned with neutron resonance-capture phenomena; he did not reference Perrin, and does not appear to have estimated a critical mass. For English-language readers, the most interesting impact of Perrin’s work can be found in a paper published in October, 1939, by Rudolf Peierls [12]. Peierls, who explicitly referenced Perrin, simplified the situation by working with pure uranium and no tamper, took an integral-equation approach, and developed approximate expressions for the critical radius for when the number of secondary neutrons per fission is either very close to unity or very large. In the regime of practical interest, the two approximations do not differ drastically, and taking an average of his results gives a critical mass only about 14% high when compared to the results of later, more sophisticated Los Alamos diffusion theory [13]. Peierls’s paper contains no numbers: He did not estimate a critical mass.
In his memoirs, Peierls related that after refining Perrin’s calculation, he had some misgivings about publishing, and claims that he consulted with Otto Frisch on the advisability of doing so. Frisch was confident that Niels Bohr had shown that an atomic bomb was not a realistic proposition, and advised Peierls that there was no reason not to publish [14]. A few months later they would find themselves in a very different circumstance.
In the Los Alamos Primer, improved cross-section data allowed Robert Serber to estimate a critical mass of ~ 200 kg, which he reduced to ~ 60 kg upon considering a more refined boundary condition. Serber also considered a tamper, although he did not incorporate any capture-cross section for the tamper material, which changes the form of the solution for the diffusion equation from what Perrin used. Since the Primer was not (originally) intended for publication, it contains no references; we can have no idea as to what extent Serber was aware of or influenced by the work of Perrin or others. That the same problem would be considered in largely the same way by two very competent theoretical physicists is not surprising, but it is striking to see the connection from 1939 to 1943.
The overall conclusion is that Perrin conceived very clearly the concepts of both critical mass and tampering, and formulated the physics correctly but for the boundary-condition issue. The details would evolve, but by the opening days of World War II the key formulations had appeared in the open literature. In view of this, Werner Heisenberg’s initially very muddled presentation of the issue during his postwar captivity at Farm Hall remains a mystery; his claim that he never studied the question of critical mass because he did not think it possible to separate U-235 does not seem fully convincing. The mystery is only deepened by the fact that an unsigned 1942 report to German Army Ordnance seems to indicate that somebody must have looked at the issue very closely [15].
As for Perrin, he enjoyed a distinguished career after the war, remaining as a professor at the Collège de France until 1972, serving as the High-Commissioner of the French Atomic Energy Commission from 1951 to 1970 (during which time that country developed its own nuclear weapons), and being involved with the discovery of the Oklo natural reactor in 1972. He passed away in Paris on July 4, 1992.
I am grateful to former Alma College student Cory Townes for translating Perrin’s paper.
References
[1] F. Perrin, “Calcul relative aux conditions éventuelles de transmutation en chaîne de l’uranium,” Comptes Rendus 208, 1394-1396 (1939).
[2] J. Bernstein, “A memorandum that changed the world,” Am. J. Phys. 79(5), 440-446 (2011).
[3] N. Bohr, “Resonance in Uranium and Thorium Disintegrations and the Phenomenon of Nuclear Fission,” Phys. Rev. 55, 418-419 (1939).
[4] O. R. Frisch, “Physical Evidence for the Division of Heavy Nuclei under Neutron Bombardment,” Nature 143(3616), 276 (1939).
[5] A copy of Perrin’s thesis can be found at https://tel.archives-ouvertes.fr/tel-00278195/document
[6] B. C. Reed, The Physics of the Manhattan Project (3rd ed., Springer, Berlin, 2015). See Chapter 2.
[7] R. Serber, The Los Alamos Primer (Berkeley, University of California Press, 1992), Sect. 10.
[8] H. L. Anderson, E. T. Booth, J. R. Dunning, E. Fermi, G. N. Glasoe, and F. G. Slack, “The Fission of Uranium,” Phys. Rev. 55, 511-512 (1939).
[9] H. L. Anderson, E. Fermi, and H. B. Hanstein, “Production of Neutrons in Uranium Bombarded by Neutrons,” Phys. Rev. 55, 797-798 (1939).
[10] H. von Halban, F. Joliot, and L. Kowarski, “Number of Neutrons Liberated in the Nuclear Fission of Uranium,” Nature 143 (3625), 680 (1939).
[11] S. Flügge, “Kann der Energieinhalt der Atomkerne technisch nutzbar gemacht werden?” Naturwissenschaften 27, 402-410 (1939).
[12] R. Peierls, “Critical Conditions in Neutron Multiplication,” Proc. Camb. Philos. Soc. 35, 610-615 (1939).
[13] B. C. Reed, “Rudolf Peierls’ 1939 Analysis of Critical Conditions in Neutron Multiplication.” Physics & Society 37(4), 10-11 (2008).
[14] R. Peierls, Bird of Passage: Recollections of a Physicist (Princeton: Princeton University Press, 1985), 153.
[15] J. Bernstein, “Heisenberg and the Critical mass,” Am. J. Phys. 70(9), 911-916 (2002).
